今回は、ホジョセンセミナーで公開している「モデルを使って考えよう」というテーマで配信された2本の動画について、メイントピックに限定して内容を紹介したいと思います。「モデルを使って考えよう」では、コミュニケーションに関する狭い領域についてミクロな視点で、「続・モデルを使って考えよう」では購入率を題材によりマクロな視点でモデルを使って考えていきます。

ミクロな視点でのモデルを使った考え方

モデルとは、現状の市場の仕組みを簡略化したものです。ここでは洗剤に関するモデルを例に、その活用方法を解説していきます。

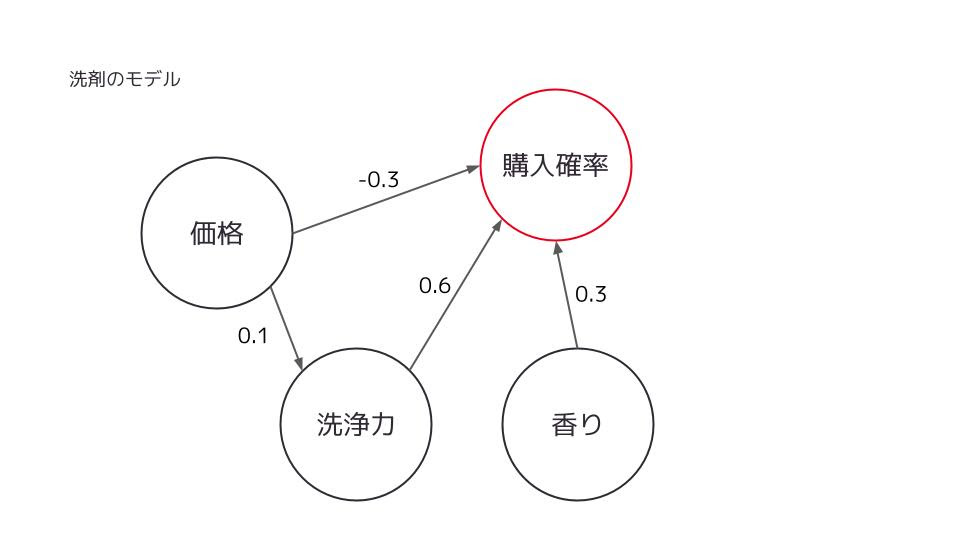
まず、このモデルにおいて「購入確率」が高まれば売上は伸長すると考えられますが、その購入確率に影響を及ぼす変数として「価格」「洗浄力」「香り」という3つの変数があります。その上で、それぞれの変数の影響力については、矢印と係数によって表されています。そうすると、このモデルから「洗浄力」や「香り」が良くなると購入確率が向上することや、「価格」が上がると購入確率が低下することが分かりますよね。では、このモデルをどのように活用していけばいいのか、というのが今回のテーマですが、結論から述べると活用方法は大きく2つ、「①モデルに従う場合」と「②モデルに抗う場合」に分けることができます。

①モデルに従う場合

これは、現状のモデルを元に、購入確率が高まるような施策を実施していくという考え方です。具体的には、モデルから現状「洗浄力」が購入確率に大きな影響力を持っていることが分かるため、製品の「洗浄力」を積極的にコミュニケーションしていくことや、「洗浄力」をウリにした製品の開発などの戦略に結びつけることなどが考えられます。

②モデルに抗う場合

これは、現状のモデルを元に、自社に都合のいいようにマーケットの構造を変化させることで、購入確率を向上させようという考え方です。その手法も、モデルのどの要素にアプローチするかという観点で3通り考えられます。

(1)係数を変える

このモデルにおいては、現状「洗浄力」の係数が0.6、「香り」の係数が0.3であることから、「洗浄力」の方が消費者の購買決定要因として大きいことが分かります。ただ、自社製品の強みが「香り」であった場合、「香り」の係数が大きい方が望ましいですよね。つまり、係数を変えるというのは、モデルに抗って各変数の重みを変化させることで、自社の売上が伸びやすい方向にマーケットの構造を変化させるということです。次に紹介する「変数を変える」は、その一つの手法でもあります。

(2)変数を変える

変数を変えるとは、新たな変数をマーケットに導入することで、マーケットの構造を変化させようという手法です。例えば、新たに「抗菌」という変数がマーケットに加わると、従来の「価格」「洗浄力」「香り」などにかかる重み、すなわち係数が変化し、マーケットの構造自体が変化することが考えられます。ただし、もちろんすでに市場に顕在化している変数ではなく、これまで意識されていなかったような変数でなければなりません。

(3)ロジックを変える

これはつまり、変数を繋ぐ「矢印」を変化させるということです。現状、モデルには「価格が高い」→「洗浄力が強い」というロジックが組み込まれていますが、新たに「洗浄力が強い」→「香りがいい」というロジックを組み込むことで、消費者の意思決定プロセス、すなわちマーケットの構造自体を変化させることができます。

このようにモデルを活用することで、自社製品の購入確率を向上させるための施策や戦略の方向性を決めやすくなるので、ブレストも行いやすくなります。


マクロな視点でのモデルを使った考え方

まず、年間購入回数が\(n\)回のカテゴリにおける、あるブランドの購入確率を\(p\)としたとき、このブランドの年間購入率を以下のようなモデルで表現してみましょう。(便宜上、非常に単純化したモデルを用いて説明しますが、実際の年間購入率は もう少し複雑なモデルで表現されることがほとんどです。)

$$1-(1-p)^n$$

ここで、\((1-p)\)がそのブランドが選ばれない確率であることから、\((1-p)^n\)は \(n\)回連続で選ばれない確率、すなわち \(1-(1-p)^n\) は 1年間で最低1回は購入してもらえる確率(=年間購入率)ということですね。

では、この「年間購入率を上げていきたいというビジネス上の課題に対して、どう取り組んでいくのか」というのが、今回のモデルを使って考えたいポイントになりますが、手法は大きく2つ考えられます。

一つは、\((1-p)\) を小さくする、すなわち \(p\)を大きくすること。そして、もう一つが、\(n\)を大きくすることです。

前者の購入確率 \(p\)を大きくすることについては、手法も含め、また別の機会に説明するとして、今回は年間購入回数 \(n\)についてのモデルを使った考え方を説明していきます。

まず、なぜ\(n\)を大きくすると年間購入率が大きくなるのかについて補足すると、\((1-p)\) は1以下であることから、\(n\)(=年間購入回数)が大きいほど、\((1-p)^n\) は 0に近づいていきますよね。すなわち、\(1-(1-p)^n\)(=年間購入率)が高くなりやすいということです。例えば、\(p\)(=購入確率)が1%の商品について、購入を検討される回数が年間50回の場合と年間2回の場合では、年間50回の方が年間購入率は高くなるということです。

つまり、このモデルから分かることは、カテゴリの年間購入回数が大きければ大きいほど、年間購入率も大きくなりやすいということです。では、この事実を、事業戦略やマーケティングプランを設計する上で、どのように役立てればいいのでしょうか。

例えば、\(p\) がかなり大きいようなメガ・ブランドであれば、逆に\(n\)を小さくするような戦略が考えられるかもしれません。マーケットにおいて\(n\)が大きいということは、\(p\)が小さなブランドにとっては、トライアル購入をしてもらいやすいことから望ましい状態と言えます。一方、すでに\( p\)が大きいようなメガ・ブランドにとっては、そういった他のブランドに移行されるリスクが高い状態とも言えますよね。そのため、メガブランドは\(n\)を下げるような戦略をとることで、自社に有利な状況を作ることができるのです。例えば、「ビールの箱売り」や「大容量の詰め替え洗剤」などは、年間購入回数\(n\)を下げる施策の一例と言えます。

この考え方は、新規市場に参入する際や、新ブランドを立ち上げる際にも当てはめることができます。例えば、年間購入回数が高い「お菓子」などであれば、トライアル購入を獲得しやすいため、参入しやすいマーケットと言えます。反対に、年間購入回数が低い「防虫剤」などについては、商品のスペックが高くても、中々トライアル購入してもらえない可能性が大いにあります。もし、宣伝広告費をかけられるのであれば 購入確率 \(p\)を上げやすくなるため、トライアル購入を十分に獲得できる可能性はありますが、宣伝広告費をかけられない状況であれば、そのマーケットにおいて成功できるかどうかは、年間購入回数\(n\)の大きさ、すなわちトライアルの獲得しやすさにも大きく左右されるということです。

このように年間購入率のモデルに基づいて考えることで、ブランドがどのような事業戦略を取るべきかを考えやすくなります。

ホジョセンのセミナーでは、他にも様々なマーケティングに関するお話をしています。過去の動画についてもご質問は大歓迎ですので、ぜひご視聴ください。