コラム
こんにちは。株式会社ホジョセンの金瀬です。
今回のコラムではちょっとした息抜きに、当たり付き自動販売機について考えてみたいと思います。
ホジョセンのオフィスビルの入口には当たり付きの自動販売機が設置されていて、弊社代表の高橋は毎日その自動販売機で飲み物を買っています。
ある日高橋から以下の課題が出されました。

僕はここ3年、毎日のように自動販売機で飲み物を買っているけど一向に当たりが出ない。金瀬さん、トレーニングがてらこの事象が起こりうるのかどうか調べてください。僕は1/999くらいの確率だとしてもいい加減当たらないのはおかしいと思う。
突然の課題ですが、この課題に取り組むに当たり、以下の順で確認していきたいと思います。
突然モデルと書くと難しく聞こえますが、例えばサイコロを振って1の目が出る確率は、「サイコロのそれぞれの目が出る確率は等しく、また1回目にサイコロを振る時も、2回目に振る時も、お互いの確率に影響しない」と言う仮定(=モデル)の中で考えられています。
「自動販売機で飲み物を1つ買う」ことを1つの独立した試行とし、「当たる」回数\(X\)が、試行回数\(n\)、「当たる」確率\(p\)の二項分布に従うと仮定します ( \(X \sim \mathrm{B} (n,p)\) )。よって\(n\)回中\(k\)回当たる確率\(P(X=k)\)は、
$$
P(X=k) = {n \choose k} p^k(1 – p)^{n – k}
$$
と仮定することができます。
ダイドードリンコさんの公式HPに、当たり付き自動販売機についての記載がありました。ダイドードリンコさんの当たり付き自動販売機での当たりは、景品表示法により売上予定総額の2%以内にするよう定められているそうです。さらに、自動販売機ごとに当選確率の設定を変えることができるようです。この数値を参考にさせてもらうと、自動販売機の当たりは当選確率が設定されており、その当選確率は最大1/50であると言えます。
とりあえず今回は 1/50(\(p=0.02\))だったらどうなるかを考えてみます。つまり、 \(p=0.02\)の時、\(n=600\)で1回も当たらない確率 \(P(X=0)\)を考えます。計算過程は省きますが、この結果、確率は0.00054%となりました。
これは99%以上の確率で発生しない事象と言えます。つまり、①や②で決めた仮定のうち、
のどちらかが考えられます。(厳密には、高橋がとても不運な人物である可能性もあるのですが)
今回は\(p=0.02\)とした母数(パラメータ)が高すぎると考え、高橋の予想している1/999の確率ならどうなるかをこれまでと同じ流れ(②~③-2として)で再検証してみます。
高橋の仮定している\(p=1/999\)で同様にシミュレーションを行ってみます。この結果、600回の購入のうち、1回も当たらない確率\(P(X=0)\)は約54.8%となりました。
今回の結果から、1度も当たりが出ないという事象が十分に起こりうると言えることが分かりました。ちなみに心情的には「ではそろそろ当たるのではないか」と思ってしまいがちですが、今回はあくまで二項分布を仮定しているので、次に自販機で当たる確率も約0.1%という絶望的な未来がこの仮定の世界では待っているわけです。
このようにこの自動販売機のテーマについて話しているときに、高橋から「そもそも各購入のインターバルって結果に影響しないのか?」とこれまでの仮定をひっくり返すような疑問が投げかけられました。

各購入のインターバルが当選に必要な条件だった場合はどうするの? 僕が自販機設置者なら、最初の購入者には当たりは出さないけどなあ。例えば、3人並んでるとしたら、1人目の購入者に当たりを出したら売上は下がるよね。前回購入者とのインターバルが短い購入者にしか当たりを出したくないね。
…なるほど、二項分布の仮定というのはこうして簡単に崩れうることが分かりました。(なかなか最低な設定の自販機ですが…)つまり、それぞれの試行が独立していないということになるので、先ほど導いた確率の前提が崩れ、そのまま適用することはできなくなります。また、新たにインターバルというパラメーターが必要になってきます。
ここから何が分かるかというと、当たり前に正しいと思って検証に使っていたモデルが、実は単なる仮説でしかないという恐ろしい事実の存在です。
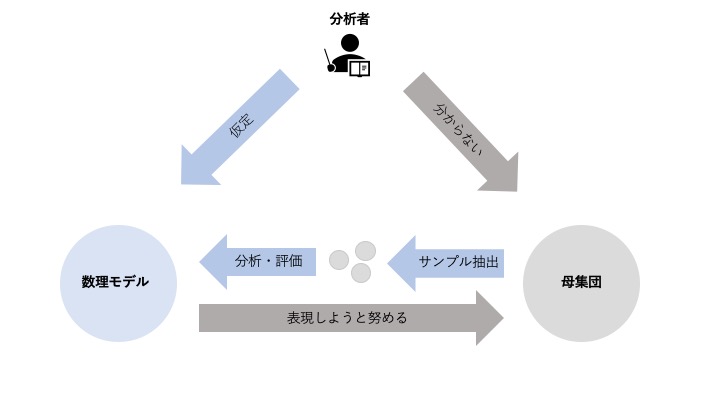
このように、私たちの分析というのは母集団からサンプルを抽出して、その「サンプル」がどのような数理モデル(分布など)に従って存在しているのかを仮定することで初めて行うことができます。
そして実際に仮定した数理モデルが真の分布に等しいかという検証は非常に難しいです(カルバック・ライブラ距離やエントロピーなどを用いての検証があるようなのですが、勉強中です…)。ですので、分析を行う際は常に、自分たちがどのような世界を仮定していて、その世界が自分たちの知りたい母集団をどの程度表現しているのかを常に意識しておく必要があります。
このようにホジョセンでは日常の様々なことに対して、確率やマーケティングの問題に置き換えて議論が起きています。おかげで私も日常生活を送りながら確率やマーケティングについて考えることが癖になってきました。
もしかしてこうした視点を植え付けるために問題が出されているのでしょうか…?
ホジョセンメルマガは、マーケティングのご質問にお答えしたり、マーケティングコラムをお届けしたり、と毎週たったの5分で読めるマーケティング情報を、毎週水曜日にお送りしています。
ホジョセンメルマガに登録
 マーケのヒント
マーケのヒント
モデルを活用してマーケティング戦略を立案する考え方
2021年8月19日 金瀬 幸子
 マーケのヒント
マーケのヒント
上市後レビューに役立つ!売れていない理由 7つのパターン~消費財編
2020年8月26日 赤間 かおり
